如图，边长为a的正方形ABCD中，点E、F分别在AB、BC上，且
，将△AED、△CFD分别沿DE、DF折起，使A、C两点重合于点
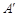，连结A¢B．
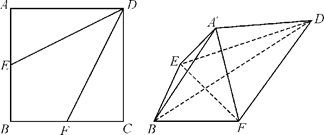
（Ⅰ）判断直线EF与A¢D的位置关系，并说明理由；
（Ⅱ）求二面角F－A¢B－D的大小．
相关试题
的前n项和为
，
，满足
是
与-3的等差中项。
的最小值和最小正周期；
.
中，
，证明：数列
是等差数列。
项和
。
是椭圆
的两个焦点，
是椭圆上的点，且
．
的周长；推荐套卷
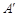如图，边长为a的正方形ABCD中，点E、F分别在AB、BC上，且，将△AED、△CFD分别沿DE、DF折起，使A、C两点重合于点，连结A¢B．
（Ⅰ）判断直线EF与A¢D的位置关系，并说明理由；
（Ⅱ）求二面角F－A¢B－D的大小．
粤公网安备 44130202000953号