某单位有
、
、
三个工作点，需要建立一个公共无线网络发射点
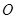，使得发射点到三个工作点的距离相等．已知这三个工作点之间的距离分别为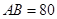
，
，
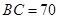
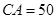
．假定、、、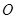四点在同一平面上．
（1）求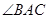
的大小；
（2）求点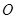到直线
的距离．
相关试题
的前
项和为
, 
.
．
的最小正周期；
，
，
与
的夹角为
.
，
；
.
，使
在闭区间
上的最大值是
？若存在，求出对应的
，
其中
，
.
的最小正周期；(2)求
上的单调递减区间.推荐套卷
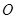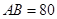
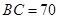
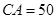
某单位有、、三个工作点，需要建立一个公共无线网络发射点，使得发射点到三个工作点的距离相等．已知这三个工作点之间的距离分别为，，．假定、、、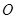四点在同一平面上．
（1）求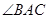的大小；
（2）求点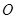到直线的距离．
粤公网安备 44130202000953号