已知椭圆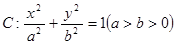
的两个焦点分别为
,且
,点
在椭圆上,且
的周长为6.
(I)求椭圆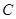
的方程;
(II)若点的坐标为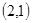
,不过原点
的直线与椭圆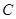相交于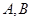
两点,设线段
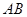的中点为
,点到直线的距离为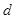
,且
三点共线.求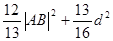
的最大值.
－
≥a＋
－2.
≥
＋
.推荐套卷
已知椭圆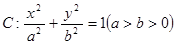的两个焦点分别为,且,点在椭圆上,且的周长为6.
(I)求椭圆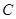的方程;
(II)若点的坐标为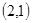,不过原点的直线与椭圆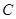相交于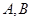两点,设线段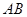的中点为,点到直线的距离为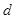,且三点共线.求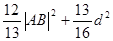的最大值.
粤公网安备 44130202000953号