如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?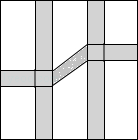
相关知识点
推荐套卷
如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?