某市准备从7名报名者（其中男5人，女3人）中选3人参加三个副局长职务竞选.
（1）设所选3人中女副局长人数为
，求的分布列及数学期望.
（2）若选派三个副局长依次到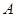
、
、
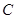三个局商上任，求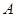局是男局长的情况下，局是女副局长的概率.
≤
≤
≤1，求证：
≤1推荐套卷
某市准备从7名报名者（其中男5人，女3人）中选3人参加三个副局长职务竞选.
（1）设所选3人中女副局长人数为，求的分布列及数学期望.
（2）若选派三个副局长依次到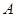、、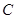三个局商上任，求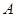局是男局长的情况下，局是女副局长的概率.
粤公网安备 44130202000953号