某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为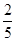 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为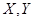 ,求
,求 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?
推荐套卷
某联欢晚会举行抽奖活动,举办方设置了甲.乙两种抽奖方案,方案甲的中奖率为 ,中将可以获得2分;方案乙的中奖率为
,中将可以获得2分;方案乙的中奖率为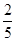 ,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
,中将可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中将与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为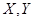 ,求
,求 的概率;
的概率;
(2)若小明.小红两人都选择方案甲或方案乙进行抽奖,问:他们选择何种方案抽奖,累计的得分的数学期望较大?