如图,点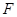 是椭圆
是椭圆 (
( )的左焦点,点
)的左焦点,点 ,
,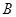 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为 ,点
,点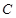 在
在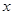 轴上,且
轴上,且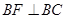 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 与由三点
与由三点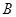 ,
,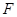 ,
,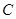 确定的圆
确定的圆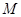 相交于
相交于 ,
,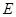 两点,满足
两点,满足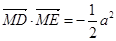 .
.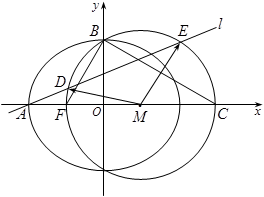
(1)若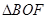 的面积为
的面积为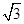 ,求椭圆的方程;
,求椭圆的方程;
(2)直线 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论.
推荐套卷
如图,点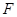 是椭圆
是椭圆 (
( )的左焦点,点
)的左焦点,点 ,
,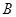 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为 ,点
,点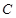 在
在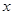 轴上,且
轴上,且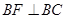 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 与由三点
与由三点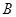 ,
,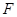 ,
,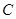 确定的圆
确定的圆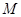 相交于
相交于 ,
,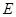 两点,满足
两点,满足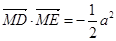 .
.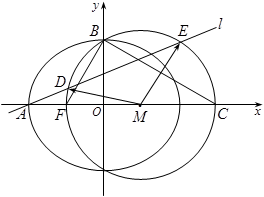
(1)若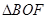 的面积为
的面积为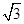 ,求椭圆的方程;
,求椭圆的方程;
(2)直线 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论.