2010年亚运会在中国广州举办, 期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)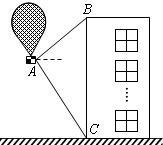
(参考数据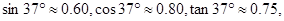
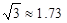 )
)
相关知识点
推荐套卷
2010年亚运会在中国广州举办, 期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
(参考数据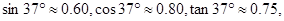
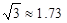 )
)