某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
| 版本 |
人教A版 |
人教B版 |
||
| 性别 |
男教师 |
女教师 |
男教师 |
女教师 |
| 人数 |
6 |
 |
4 |
 |
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是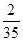 .且
.且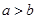 .
.
(1)求实数 ,
, 的值
的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为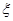 ,求随机变量
,求随机变量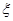 的分布列和数学期望
的分布列和数学期望 .
.
推荐套卷
 ,试判断函数
,试判断函数 在(0,+∞)上的单调性,并加以证明。
在(0,+∞)上的单调性,并加以证明。
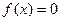 有两不相等的正根,求
有两不相等的正根,求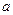 的取值范围;
的取值范围;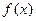 满足
满足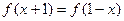 ,求函数在
,求函数在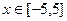 的最大值和最小值;
的最大值和最小值;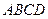 如图所示,
如图所示,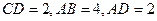
 上有一点
上有一点 ,过点
,过点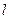 ,当点
,当点 运动到点
运动到点 时,
时,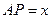 ,
,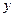 ,试写出
,试写出 的函数.
的函数.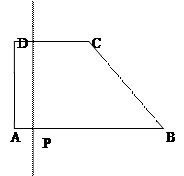
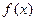 是定义在(0,+∞)上的减函数,且有
是定义在(0,+∞)上的减函数,且有
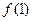 的值
的值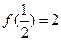 ,求不等式
,求不等式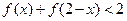 的解集。
的解集。 粤公网安备 44130202000953号
粤公网安备 44130202000953号