已知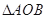
的顶点A在射线
上，
、
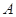两点关于x轴对称，0为坐标原点，且线段AB上有一点M满足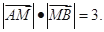
当点A在
上移动时，记点M的轨迹为W.
（Ⅰ）求轨迹W的方程；
（Ⅱ）设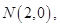
是否存在过
的直线
与W相交于P,Q两点，使得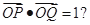
若存在，
求出直线；若不存在，说明理由.
、
，求
的值？
时，不等式：
恒成立，求实数
的范围．
，求
的最大值；
及
的值域；推荐套卷
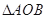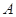已知的顶点A在射线上，、两点关于x轴对称，0为坐标原点，且线段AB上有一点M满足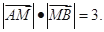当点A在上移动时，记点M的轨迹为W.
（Ⅰ）求轨迹W的方程；
（Ⅱ）设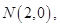是否存在过的直线与W相交于P,Q两点，使得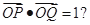若存在，
求出直线；若不存在，说明理由.
粤公网安备 44130202000953号