已知抛物线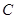
:
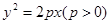上横坐标为4的点到焦点的距离为5．
（Ⅰ）求抛物线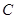的方程；
（Ⅱ）设直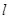线
与抛物线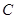交于不同两点
，若满足
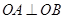，证明直线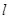恒过定点，并求出定点
的坐标．
（Ⅲ）试把问题（Ⅱ）的结论推广到任意抛物线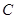: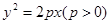中，请写出结论，不用证明．
．
．
行里的最后一个数字是多少？
对一切正整数
都成立，那么
的值为多少？
．推荐套卷
已知抛物线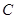: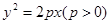上横坐标为4的点到焦点的距离为5．
（Ⅰ）求抛物线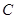的方程；
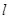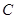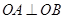（Ⅱ）设直线与抛物线交于不同两点，若满足，证明直线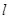恒过定点，并求出定点的坐标．
（Ⅲ）试把问题（Ⅱ）的结论推广到任意抛物线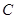: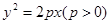中，请写出结论，不用证明．
粤公网安备 44130202000953号