已知椭圆E：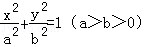
的离心率为
，右焦点为F，且椭圆E上的点到点F距离的最小值为2．
（1）求椭圆E的方程；
（2）设椭圆E的左、右顶点分别为A，B，过点A的直线l与椭圆E及直线x=8分别相交于点M，N．
（ⅰ）当过A，F，N三点的圆半径最小时，求这个圆的方程；
（ⅱ）若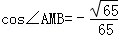
，求△ABM的面积．
，问方程
在区间[－1，0]内是否有
在(0,1)内恰有一解，求实数
的取值范围．
，求
的值.
终边上一点
的坐标为
，
；
求
的值。
推荐套卷
已知椭圆E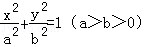：的离心率为，右焦点为F，且椭圆E上的点到点F距离的最小值为2．
（1）求椭圆E的方程；
（2）设椭圆E的左、右顶点分别为A，B，过点A的直线l与椭圆E及直线x=8分别相交于点M，N．
（ⅰ）当过A，F，N三点的圆半径最小时，求这个圆的方程；
（ⅱ）若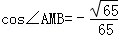，求△ABM的面积．
粤公网安备 44130202000953号