国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.根据以上信息,解答下列问题:


(1)该校随机抽查的学生中每天在校锻炼时间超过1小时的人数是 ;
(2)请将图2补充完整;
(3)2013年该市初中毕业生约为6.4万人,请你估计今年该市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人?
相关知识点
推荐套卷
 与
与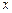 轴的两个交点
轴的两个交点 =,b=,顶点C的坐标为;
=,b=,顶点C的坐标为; 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
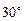 角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转
角的三角板ABC和DEC如图①摆放,使直角顶点重合. 将图①中△DEC绕点C逆时针旋转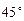 得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
得△D1E1C,点F、G、H的对应点分别为F1、G1、H1,如图③.探究线段D1F1与AH1之间的数量关系,并写出推理过程;
 (3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.
(3)在(2)的条件下,若D1E1与CE交于点I,求证:G1I =CI.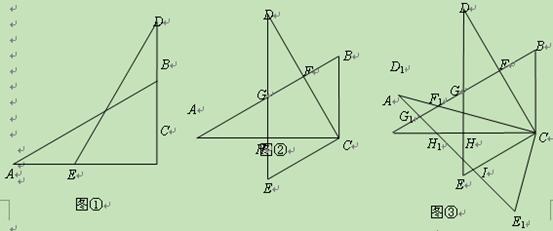
 轴交于点C,与双曲线
轴交于点C,与双曲线 交于A(3,
交于A(3,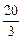 )、B(-5,
)、B(-5, )两点.AD⊥
)两点.AD⊥ 轴交于点E.
轴交于点E.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号