作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为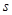 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)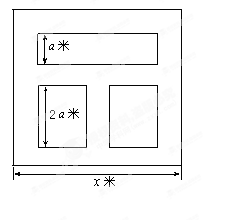
(1)试将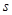 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积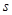 取得最大值.
取得最大值.
推荐套卷
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为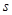 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
(1)试将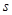 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积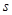 取得最大值.
取得最大值.