设椭圆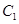 与抛物线
与抛物线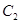 的焦点均在
的焦点均在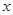 轴上,
轴上,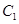 的中心及
的中心及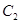 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
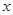 |
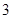 |
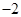 |
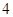 |
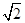 |
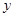 |
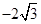 |
 |
 |
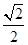 |
(Ⅰ)求曲线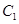 、
、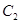 的标准方程;
的标准方程;
(Ⅱ)设直线 过抛物线
过抛物线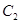 的焦点
的焦点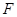 ,
,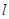 与椭圆交于不同的两点
与椭圆交于不同的两点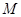 、
、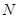 ,当
,当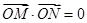 时,求直线
时,求直线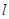 的方程.
的方程.
推荐套卷
设椭圆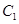 与抛物线
与抛物线 的焦点均在
的焦点均在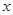 轴上,
轴上,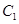 的中心及
的中心及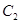 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
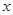 |
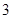 |
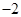 |
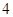 |
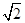 |
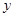 |
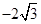 |
 |
 |
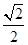 |
(Ⅰ)求曲线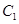 、
、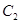 的标准方程;
的标准方程;
(Ⅱ)设直线 过抛物线
过抛物线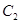 的焦点
的焦点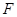 ,
,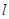 与椭圆交于不同的两点
与椭圆交于不同的两点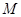 、
、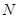 ,当
,当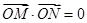 时,求直线
时,求直线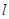 的方程.
的方程.