如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.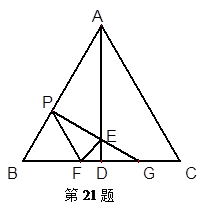
(1)①填空:如果BP=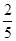 ,则BG= ;
,则BG= ;
②用x的代数式表示线段DG的长,并直接写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式。
(3)当以P、E、F为顶点的三角形与△EDG相似时,请求出BP的长。
相关知识点
推荐套卷
如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过P点作PF//AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设BP=x.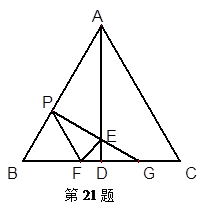
(1)①填空:如果BP=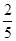 ,则BG= ;
,则BG= ;
②用x的代数式表示线段DG的长,并直接写出自变量x的取值范围;
(2)记△DEF的面积为S,求S与x之间的函数关系式。
(3)当以P、E、F为顶点的三角形与△EDG相似时,请求出BP的长。