小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 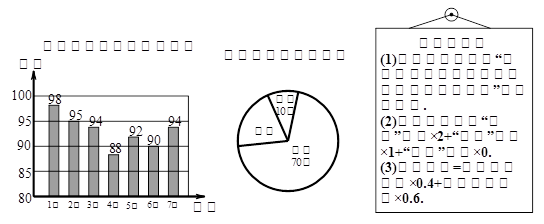
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
相关知识点
推荐套卷
小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 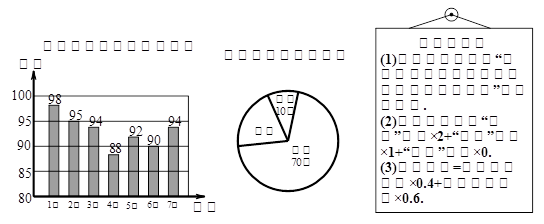
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?