某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，对往年的市场行情和生产情况进行了调查，提供了如下两个信息图，如甲、乙两图。
注：甲、乙两图中的A、B、C、D、E、F、G、H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本（生产成本6月份最低，甲图的图象是线段，乙图的图象是抛物线的一部分）。请你根据图象提供的信息说明：
（1）在3月份出售这种蔬菜，每千克的收益是多少元？（收益＝售价－成本）
（2）哪个月出售这种蔬菜，每千克的收益最大？最大收益是多少？说明理由。
如图，在平面直角坐标系
中，矩形
的边
在
轴上，且
，
，直线
经过点
，交
轴于点
．
（1）点、
的坐标分别是（），（）；
（2）求顶点在直线上且经过点
的抛物线的解析式；
（3）将（2）中的抛物线沿直线向上平移，平移后的抛物线交轴于点
，顶点为点
．求出当
时抛物线的解析式．
如图，在△ABC中，AB=4，AC=3，D、E分别是AB、AC上的动点，在边AC上取一点E，使A、D、E三点组成的三角形与△ABC相似．
（1）当AD=2时，求AE的长；
（2）当AD=3时，求AE的长；
（3）通过上面两题的解答，你发现了什么？
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯．在雷达显示图上，标明了三艘海监船的坐标为O（0，0）、B（80，0）、C（80，60），（单位：海里）三艘海监船安装有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域（只考虑在海平面上的探测）．
（1）若在三艘海监船组成的△OBC区域内没有探测盲点，则雷达的有效探测半径r至少为_______海里；
（2）某时刻海面上出现一艘菲律宾海警船A，在海监船C测得点A位于南偏东60°方向上，同时在海监船B测得A位于北偏东45°方向上，海警船A正以每小时20海里的速度向正西方向移动，我海监船B立刻向北偏东15°方向运动进行拦截，问我海监船B至少以多少速度才能在此方向上拦截到菲律宾海警船A？
在某校八（1）班组织了无锡欢乐义工活动，就该班同学参与公益活动情况作了一次调查统计．如图是一同学通过收集数据后绘制的两幅不完整的统计图．请根据图中提供的信息，解答下列问题：
（1）该班共有______名学生，其中经常参加公益活动的有_____名学生；
（2）将频数分布直方图补充完整；
（3）若该校八年级有600名学生，试估计该年级从不参加的人数．若我市八年级有21000名学生，能否由此估计出我市八年级学生从不参加的人数，为什么？
（4）根据统计数据，你想对你的同学们说些什么？
．
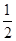粤公网安备 44130202000953号