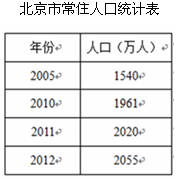
北京市近年来大力发展绿地建设，2010年人均公共绿地面积比2005年增加了4平方米，以下是根据北京市常住人口调查数据和绿地面积的有关数据制作的统计图表的一部分．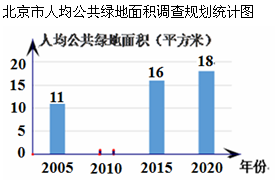
（1）补全条形统计图，并在图中标明相应数据；
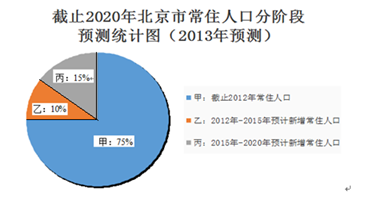
（2）按照2013年的预测，预计2020年北京市常住人口将达到多少万人？
（3）按照2013年的北京市常住人口预测，要完成2020年的北京市人均公共绿地面积规划，从2005年到2020年，北京市的公共绿地总面积需增加多少万平方米？
相关试题
与
在平面直角坐标系中的位置如图.
⑴分别写出下列各点的坐标：
； 
；
；
⑵说明由经过怎样的平移得到 ．
⑶若点
（
，
）是内部一点，则平移后内的对应点
的坐标为；
⑷求的面积.
∠2，∠1+∠2=162°，求∠3与∠4的度数．
求
的算术平方根.相关知识点
推荐套卷
粤公网安备 44130202000953号