如图所示，要用栏杆围成一个面积为50平方米的长方形花园，其中有一面靠墙不需要栏杆，其中正面栏杆造价每米200元，两个侧面栏杆每米造价50元，设正面栏杆长度为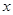
米.
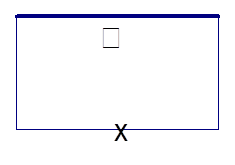
（1）将总造价y表示为关于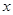的函数；
（2）问花园如何设计，总造价最少？并求最小值.
相关试题
的前
项和
，且
成等差数列．
的前n项和
，求得
成立的n的最小值．
中，
求数列
证明：
满足
，且
成等差数列．
的值和
，求数列
的前
项和．
，
是曲线
在点
处的切线与x轴交点的横坐标．
的通项公式；
，证明
．
的前n项和为
．已知
．
满足
，求
．推荐套卷
如图所示，要用栏杆围成一个面积为50平方米的长方形花园，其中有一面靠墙不需要栏杆，其中正面栏杆造价每米200元，两个侧面栏杆每米造价50元，设正面栏杆长度为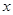米.
（1）将总造价y表示为关于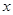的函数；
（2）问花园如何设计，总造价最少？并求最小值.
粤公网安备 44130202000953号