(理科)椭圆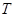 的中心为坐标原点
的中心为坐标原点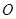 ,右焦点为
,右焦点为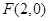 ,且椭圆
,且椭圆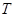 过点
过点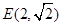 。
。 的三个顶点都在椭圆
的三个顶点都在椭圆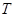 上,设三条边的中点分别为
上,设三条边的中点分别为 .
.
(1)求椭圆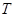 的方程;
的方程;
(2)设 的三条边所在直线的斜率分别为
的三条边所在直线的斜率分别为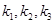 ,且
,且 。若直线
。若直线 的斜率之和为0,求证:
的斜率之和为0,求证: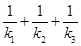 为定值.
为定值.
推荐套卷
(理科)椭圆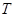 的中心为坐标原点
的中心为坐标原点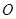 ,右焦点为
,右焦点为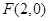 ,且椭圆
,且椭圆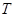 过点
过点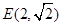 。
。 的三个顶点都在椭圆
的三个顶点都在椭圆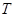 上,设三条边的中点分别为
上,设三条边的中点分别为 .
.
(1)求椭圆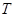 的方程;
的方程;
(2)设 的三条边所在直线的斜率分别为
的三条边所在直线的斜率分别为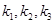 ,且
,且 。若直线
。若直线 的斜率之和为0,求证:
的斜率之和为0,求证: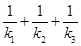 为定值.
为定值.