如图（1）是某种台灯的示意图，灯柱BC固定垂直于桌面，AB是转轴，可以绕着点B按顺时针方向转动，AB=10cm，BC=20cm，圆锥形灯罩的轴截面△APQ是等腰直角三角形，∠PAQ=90°，且PQ∥AB．转动前，点A、B、C在同一直线上．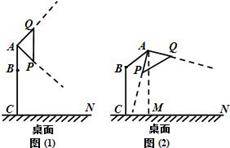
（1）转动AB，如图（2）所示，若灯心A到桌面的距离AM=25cm，求∠ABC的大小；
（2）继续转动AB，当光线AP第一次经过点C，求此时灯心A到桌面的距离AM长．（假设桌面足够大）
相关试题
某弹簧的自然长度为3cm,在弹簧限度内,所挂物体的质量x每增加1kg,弹簧长度y增加0.5cm.
（1）计算所挂物体的质量分别为1kg、2kg、3kg、4kg、5kg时的弹簧长度,并填入下表:
| x/kg |
0 |
1 |
2 |
3 |
4 |
5 |
| y/cm |
（2）你能写出x与y之间的关系式吗?
，
，
，-8，
，π，0.3737737773…….分别填入相应的集合中.
相关知识点
推荐套卷
粤公网安备 44130202000953号