如图, 为圆
为圆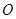 的直径,点
的直径,点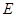 、
、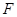 在圆
在圆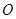 上,
上,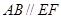 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 所在的平面互相垂直,且
所在的平面互相垂直,且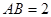 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设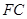 的中点为
的中点为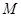 ,求证:
,求证: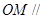 平面
平面 ;
;
(3)设平面 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求
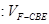 .
.
推荐套卷
如图, 为圆
为圆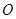 的直径,点
的直径,点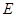 、
、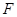 在圆
在圆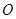 上,
上,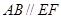 ,矩形
,矩形 所在的平面和圆
所在的平面和圆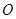 所在的平面互相垂直,且
所在的平面互相垂直,且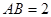 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设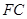 的中点为
的中点为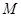 ,求证:
,求证: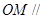 平面
平面 ;
;
(3)设平面 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求
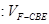 .
.