如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A、D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O).
(1)求此抛物线的解析式;
(2)过点P作CB所在直线的垂线,垂足为点R;
①求证:PF=PR
②是否存在点P,使得△PFR为等边三角形;若存在,求出点P的坐标,若不存在,请说明理由.
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为点S,试判断△RSF的形状.
相关知识点
推荐套卷

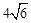 ,求BG的长.
,求BG的长.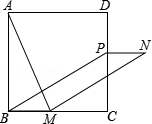
 粤公网安备 44130202000953号
粤公网安备 44130202000953号