在△ABC中,∠A=∠B=30°,AB=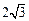 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.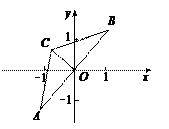
(1) 当点B在第一象限,纵坐标是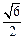 时,求点B的横坐标;
时,求点B的横坐标;
(2) 如果抛物线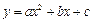 (a≠0)的对称轴经过点C,请你探究:
(a≠0)的对称轴经过点C,请你探究:
当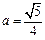 ,
,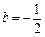 ,
,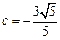 时,A,B两点是否都在这条抛物线上?并说明理由
时,A,B两点是否都在这条抛物线上?并说明理由
在△ABC中,∠A=∠B=30°,AB=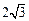 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O(如图),△ABC可以绕点O作任意角度的旋转.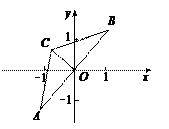
(1) 当点B在第一象限,纵坐标是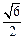 时,求点B的横坐标;
时,求点B的横坐标;
(2) 如果抛物线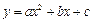 (a≠0)的对称轴经过点C,请你探究:
(a≠0)的对称轴经过点C,请你探究:
当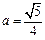 ,
,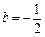 ,
,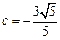 时,A,B两点是否都在这条抛物线上?并说明理由
时,A,B两点是否都在这条抛物线上?并说明理由