直线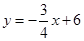 与坐标轴分别交于
与坐标轴分别交于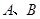 两点,动点
两点,动点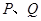 同时从
同时从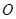 点出发,同时到达
点出发,同时到达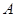 点,运动停止.点
点,运动停止.点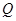 沿线段
沿线段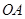 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点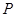 沿路线
沿路线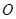 →
→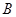 →
→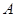 运动.
运动.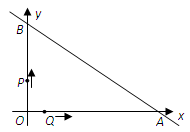
(1)直接写出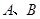 两点的坐标;
两点的坐标;
(2)设点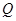 的运动时间为
的运动时间为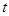 秒,
秒,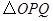 的面积为
的面积为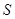 ,求出
,求出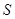 与
与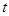 之间的函数关系式;
之间的函数关系式;
(3)当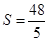 时,求出点
时,求出点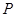 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点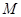 的坐标.
的坐标.
相关知识点
推荐套卷
直线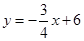 与坐标轴分别交于
与坐标轴分别交于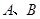 两点,动点
两点,动点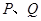 同时从
同时从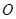 点出发,同时到达
点出发,同时到达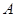 点,运动停止.点
点,运动停止.点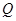 沿线段
沿线段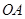 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点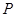 沿路线
沿路线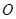 →
→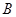 →
→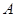 运动.
运动.
(1)直接写出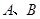 两点的坐标;
两点的坐标;
(2)设点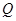 的运动时间为
的运动时间为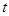 秒,
秒,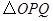 的面积为
的面积为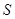 ,求出
,求出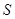 与
与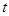 之间的函数关系式;
之间的函数关系式;
(3)当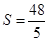 时,求出点
时,求出点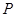 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点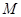 的坐标.
的坐标.