某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校1 000
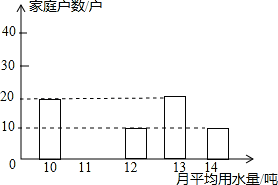
名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图.
(1)本次调查抽取的人数为_______人,估计全校同学在暑假期间平均每天做家务活的时间在30分钟以上(含30分钟)的人数为_______人;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、丙两名同学的概率.
相关知识点
推荐套卷
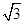 ≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)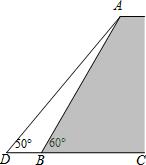
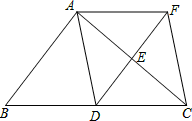
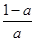 ÷
÷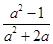 ,其中a=-
,其中a=-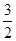 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号