在建筑楼梯时，设计者要考虑楼梯的安全程度，如图(1)，虚线为楼梯的倾斜度，斜度线与地面的夹角为倾角
，一般情况下，倾角越小，楼梯的安全程度越高；如图(2)设计者为了提高楼梯的安全程度，要把楼梯的倾角
1减至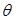
2，这样楼梯所占用地板的长度由d1增加到d2，已知d1＝4米，∠
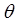1＝40°，∠2＝36°，楼梯占用地板的长度增加了多少米？(计算结果精确到0.01米，参考数据：tan40°＝0.839，tan36°＝0.727)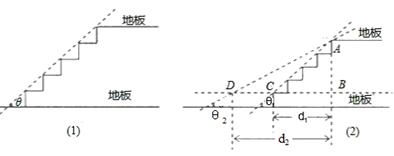
相关知识点
推荐套卷
在建筑楼梯时，设计者要考虑楼梯的安全程度，如图(1)，虚线为楼梯的倾斜度，斜度线与地面的夹角为倾角，一般情况下，倾角越小，楼梯的安全程度越高；如图(2)设计者为了提高楼梯的安全程度，要把楼梯的倾角1减至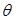2，这样楼梯所占用地板的长度由d1增加到d2，已知d1＝4米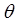，∠1＝40°，∠2＝36°，楼梯占用地板的长度增加了多少米？(计算结果精确到0.01米，参考数据：tan40°＝0.839，tan36°＝0.727)
粤公网安备 44130202000953号