以直角坐标系的原点O为极点，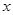
轴的正半轴为极轴，已知点P的直角坐标为（1，－5），点M的极坐标为（4，
），若直线
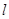过点P，且倾斜角为
，圆C以M为圆心，4为半径。
（I）求直线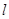的参数方程和圆C的极坐标方程。
（II）试判定直线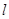与圆C的位置关系。
（2）
（3）
与直线
及
所围成图形的面积.
做直线运动，式中
为时间t内通过的距离，媒质的阻力与速度的平方成正比（比例常数为
），试求物体由
运动到
时，阻力所做的功.
的正三角形的厚纸，从这块厚纸的三个角，按右图那样切下三个全等的四边形后，做成一个无盖的盒子，要使这个盒子容积最大，
值应为多少？推荐套卷
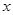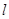以直角坐标系的原点O为极点，轴的正半轴为极轴，已知点P的直角坐标为（1，－5），点M的极坐标为（4，），若直线过点P，且倾斜角为，圆C以M为圆心，4为半径。
（I）求直线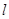的参数方程和圆C的极坐标方程。
（II）试判定直线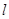与圆C的位置关系。
粤公网安备 44130202000953号