已知平面上动点P(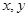 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为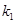 、
、 且
且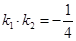
(I)求动点P所在曲线C的方程。
(II)设直线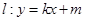 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线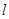 的距离。(O为坐标原点)
的距离。(O为坐标原点)
推荐套卷
已知平面上动点P(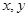 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为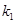 、
、 且
且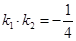
(I)求动点P所在曲线C的方程。
(II)设直线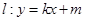 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线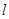 的距离。(O为坐标原点)
的距离。(O为坐标原点)