函数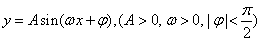
的最小值是
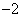，在一个周期内图象最高点与最低点横坐标差是
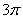，又：图象过点
，
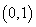求（1）函数解析式，
（2）函数的最大值、以及达到最大值时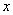
的集合；
（3）该函数图象可由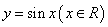
的图象经过怎样的平移和伸缩得到？
（4）当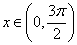
时，函数的值域.
相关试题
是定义在
上的奇函数，当
时，
。
及
的值；
=
（ex-1）。
或
，分别求满足下列条件的实数m的取值范围：
的最小值；
．
，写出数列
的前5项；
．推荐套卷
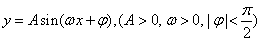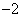函数的最小值是，在一个周期内图象最高点与最低点横坐标差是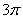，又：图象过点，
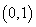求（1）函数解析式，
（2）函数的最大值、以及达到最大值时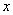的集合；
（3）该函数图象可由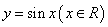的图象经过怎样的平移和伸缩得到？
（4）当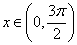时，函数的值域.
粤公网安备 44130202000953号