阅读下面材料：根据两角和与差的正弦公式，有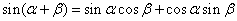
----------①
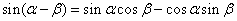------②
由①+② 得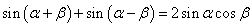
------③
令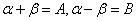
有
代入③得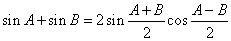 
．
（1）利用上述结论，试求
的值。
（2）类比上述推证方法，根据两角和与差的余弦公式，证明: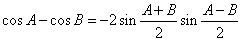
;
相关试题
中，
是平行四边形，
，
分别是
，
的中点．
平面
．
、
、
分别为空间四边形
的边
，
，
上的点，且
．
平面
，
平面
的交线
．
中，求证：平面
平面
．
中，试作出过
且与直线
平行的截面，并说明理由．
的边长为
，平面
到正方形各顶点的距离都是
，
分别是
，
上的点，且
．
平面
；
的长．
相关知识点
推荐套卷
阅读下面材料：根据两角和与差的正弦公式，有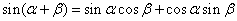 ----------① 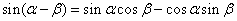------②
由①+② 得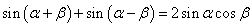 ------③
令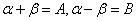 有
代入③得 ．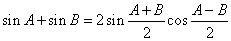
（1）利用上述结论，试求的值。
（2）类比上述推证方法，根据两角和与差的余弦公式，证明:;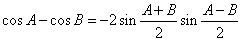
粤公网安备 44130202000953号