在矩形ABCD中，|AB|=2
，|AD|=2，E、F、G、H分别为矩形四条边的中点，以HF、GE所在直线分别为x，y轴建立直角坐标系(如图所示)．若R、R′分别在线段0F、CF上，且
=
=
.
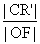(Ⅰ)求证：直线ER与GR′的交点P在椭圆
：
+
=1上；
(Ⅱ)若M、N为椭圆上的两点，且直线GM与直线GN的斜率之积为
，求证：直线MN过定点；并求△GMN面积的最大值．
中，已知
，
．
与公差
，并写出通项公式；
？
中，
，
，
．
成等比数列； （2）求
．
，曲线
和
有4个不同的交点．
的取值范围；
与
轴两交点
．
为直径的圆
的方程；
的顶点在圆
应满足什么条件．
表示两条直线，求实数
的值．推荐套卷
在矩形ABCD中，|AB|=2，|AD|=2，E、F、G、H分别为矩形四条边的中点，以HF、GE所在直线分别为x，y轴建立直角坐标系(如图所示)．若R、R′分别在线段0F、CF上，且==.
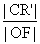(Ⅰ)求证：直线ER与GR′的交点P在椭圆：+=1上；
(Ⅱ)若M、N为椭圆上的两点，且直线GM与直线GN的斜率之积为，求证：直线MN过定点；并求△GMN面积的最大值．
粤公网安备 44130202000953号