已知函数f(x）="ax3" + x2 - ax (
且a
).
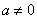(I) 若函数f(x)在{-∞，-1)和（
，+∞)上是增函数¥在（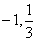
)上 是减函数，求a的值；
(II)讨论函数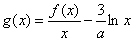
的单调递减区间；
(III)如果存在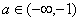
，使函数h(x)="f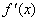(x)+" 
,x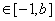
(b> - 1)，在x = -1处取得最小值，试求b的最大值.
是两个不共线的向量，
，若A、B、D三点共线，求k的值.。
．
．推荐套卷
已知函数f(x）="ax3" + x2 - ax (且a).
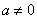(I) 若函数f(x)在{-∞，-1)和（，+∞)上是增函数¥在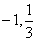（)上 是减函数，求a的值；
(II)讨论函数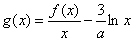的单调递减区间；
(III)如果存在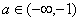，使函数h(x)="f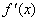(x)+" ,x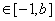 (b> - 1)，在x = -1处取得最小值，试求b的最大值.
粤公网安备 44130202000953号