(本题满分14分)
如图所示,在正三棱柱ABC -A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点。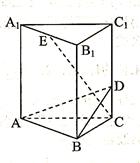
(I)求证:A1B1//平面ABD;
(II)求证:AB⊥CE;
(III)求三棱锥C-ABE的体积。
推荐套卷
(本题满分14分)
如图所示,在正三棱柱ABC -A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点。
(I)求证:A1B1//平面ABD;
(II)求证:AB⊥CE;
(III)求三棱锥C-ABE的体积。