某中学组织全校4 000名学生进行了民族团结知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图6的频数分布表和频数分布直方图(不完整).

请根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)上述学生成绩的中位数落在哪一组范围内?
(4)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校4 000名学生中约有多少名获奖?
相关知识点
推荐套卷



 被直线
被直线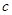 所截,
所截, ∥
∥ ,如果
,如果 ,求∠1的度数。
,求∠1的度数。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号