如图，已知一次函数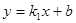
与反比例函数
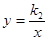的图象交于两点A(-1，6)，B(a，3)．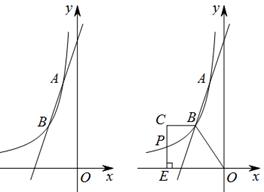
（1）求两个函数的解析式；
（2）结合图形，直接写出时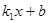
-
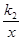﹥0时
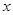的取值范围；
（3）如图2，梯形OBCE中，BC∥OE，过点C作CE⊥x轴于点E，CE和反比例函数的图象交于点P，当梯形OBCE的面积为9时，请求出点P的坐标．
，其中
．
的方程
的解为2，求代数式
的值．
，其中
，
，
．
，其中
，
．
．相关知识点
推荐套卷
如图，已知一次函数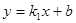与反比例函数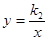的图象交于两点A(-1，6)，B(a，3)．
（1）求两个函数的解析式；
（2）结合图形，直接写出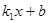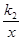时-﹥0时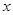的取值范围；
（3）如图2，梯形OBCE中，BC∥OE，过点C作CE⊥x轴于点E，CE和反比例函数的图象交于点P，当梯形OBCE的面积为9时，请求出点P的坐标．
粤公网安备 44130202000953号