在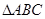 中,
中,  , 将
, 将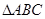 绕点
绕点 顺时针旋转角
顺时针旋转角 , 得
, 得 ,
, 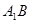 交
交 于点
于点 ,
, 分别交
分别交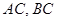 于
于 两点.
两点.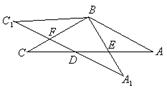
(1) 在旋转过程中, 线段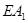 与
与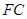 有怎样的数量关系? 证明你的结论;
有怎样的数量关系? 证明你的结论;
(2) 当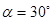 时, 试判断四边形
时, 试判断四边形 的形状, 并说明理由;
的形状, 并说明理由;
(3) 在(2)的情况下, 求线段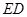 的长.
的长.
相关知识点
推荐套卷
在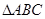 中,
中,  , 将
, 将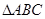 绕点
绕点 顺时针旋转角
顺时针旋转角 , 得
, 得 ,
, 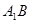 交
交 于点
于点 ,
, 分别交
分别交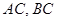 于
于 两点.
两点.
(1) 在旋转过程中, 线段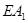 与
与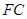 有怎样的数量关系? 证明你的结论;
有怎样的数量关系? 证明你的结论;
(2) 当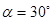 时, 试判断四边形
时, 试判断四边形 的形状, 并说明理由;
的形状, 并说明理由;
(3) 在(2)的情况下, 求线段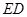 的长.
的长.