如图① ,在△ABC中,AB=AC=4,∠BAC=90o,AD⊥BC,垂足为D.
(1)S△ABD = .(直接写出结果)
(2)如图②,将△ABD绕点D按顺时针方向旋转得到△A′B′D,设旋转角为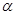 (
(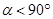 ),在旋转过程中:
),在旋转过程中:
探究一:四边形APDQ的面积是否随旋转而变化?说明理由
探究二:当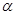 的度数为多少时,四边形APDQ是正方形?说明理由.
的度数为多少时,四边形APDQ是正方形?说明理由.
相关知识点
推荐套卷
如图① ,在△ABC中,AB=AC=4,∠BAC=90o,AD⊥BC,垂足为D.
(1)S△ABD = .(直接写出结果)
(2)如图②,将△ABD绕点D按顺时针方向旋转得到△A′B′D,设旋转角为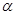 (
(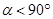 ),在旋转过程中:
),在旋转过程中:
探究一:四边形APDQ的面积是否随旋转而变化?说明理由
探究二:当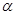 的度数为多少时,四边形APDQ是正方形?说明理由.
的度数为多少时,四边形APDQ是正方形?说明理由.