如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F. 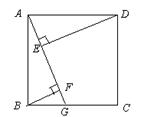
(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).
相关知识点
推荐套卷
如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F. 
(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).