在关于人体脂肪含量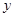 (百分比)和年龄
(百分比)和年龄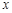 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年龄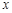 |
23 |
27 |
39 |
41 |
45 |
50 |
脂肪含量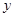 |
9.5 |
17.8 |
21.2 |
25.9 |
27.5 |
28.2 |
(Ⅰ)画出散点图,判断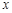 与
与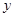 是否具有相关关系;
是否具有相关关系;
(Ⅱ)通过计算可知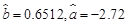 ,
,
请写出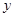 对
对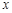 的回归直线方程,并计算出
的回归直线方程,并计算出 岁和
岁和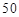 岁的残差.
岁的残差.
推荐套卷
在关于人体脂肪含量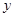 (百分比)和年龄
(百分比)和年龄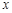 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年龄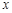 |
23 |
27 |
39 |
41 |
45 |
50 |
脂肪含量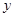 |
9.5 |
17.8 |
21.2 |
25.9 |
27.5 |
28.2 |
(Ⅰ)画出散点图,判断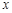 与
与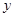 是否具有相关关系;
是否具有相关关系;
(Ⅱ)通过计算可知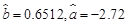 ,
,
请写出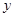 对
对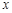 的回归直线方程,并计算出
的回归直线方程,并计算出 岁和
岁和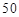 岁的残差.
岁的残差.