已知数列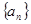
是等差数列，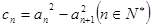
（1）判断数列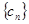
是否是等差数列，并说明理由；
（2）如果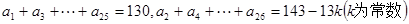
，试写出数列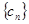的通项公式；
（3）在（2）的条件下，若数列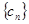得前n项和为
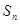，问是否存在这样的实数
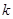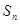，使当且仅当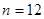
时取得最大值。若存在，求出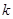的取值范围；若不存在，说明理由。
相关试题
为椭圆
的左、右焦点，
是坐标原点，过
作垂直于
轴的直线
交椭圆于
.
的方程；
的直线
与椭圆
、
两点，若
，求直线
：“方程
有两个实数根”；命题
：“方程
无实根”，若
为假，
为假，求实数
的取值范围.
.
；
图象上的点
处的切线方程.
，
，
，其中
且
.
的导函数
的最小值；
时，求函数
的单调区间及极值；
，函数
，求实数
的取值范围.
时，
，
;
与
的关系，并用数学归纳法证明.推荐套卷
已知数列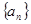是等差数列，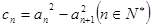
（1）判断数列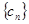是否是等差数列，并说明理由；
（2）如果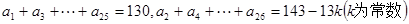，试写出数列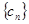的通项公式；
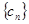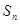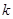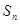（3）在（2）的条件下，若数列得前n项和为，问是否存在这样的实数，使当且仅当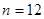时取得最大值。若存在，求出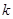的取值范围；若不存在，说明理由。
粤公网安备 44130202000953号