甲、乙两观光船分别从 、
、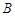 两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达
两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达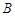 港.下图表示甲观光船距
港.下图表示甲观光船距 港的距离
港的距离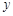 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,结合图象解答下列问题:
(小时)之间的函数关系式,结合图象解答下列问题: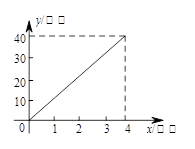
(1) 、
、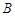 两港距离 千米,船在静水中的速度为 千米/小时;
两港距离 千米,船在静水中的速度为 千米/小时;
(2)在同一坐标系中画出乙船距 港的距离
港的距离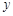 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象;
(小时)之间的函数图象;
(3)求出发几小时后,两船相距5千米.
相关知识点
推荐套卷

 ,且菱形
,且菱形


 粤公网安备 44130202000953号
粤公网安备 44130202000953号