某种产品的广告费支出
与销售额
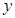（单位：百万元）之间有如下对应数据：
|
2 |
4 |
5 |
6 |
8 |
|
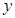30 |
40 |
60 |
50 |
70 |
（1）求回归直线方程。
（2）试预测广告费支出为10百万元时，销售额多大？
与
相交于
点．
表示过
与
交点
，一束光线过点
且以
的倾斜角投射到
上，经
过点
，
过点
，如果
，且
，求
，
和直线
，在坐标平面内求一点
，使
，且点
的距离为
．
，
，
，求
边所在直线的方程，以及该边上中线所在直线的方程．
推荐套卷
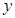某种产品的广告费支出与销售额（单位：百万元）之间有如下对应数据：
|
2 |
4 |
5 |
6 |
8 |
|
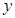30 |
40 |
60 |
50 |
70 |
（1）求回归直线方程。
（2）试预测广告费支出为10百万元时，销售额多大？
粤公网安备 44130202000953号