细心观察下图，认真分析各式，然后解答问题．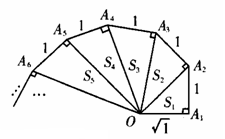
(
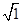)2+1=2 S1=
、(
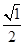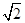)2+1=3 S2=
、（
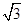)2+1=4 S3=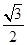
（1）推算出OA10的长；
（2）求出S12+S22+S32+…+S102的值．
，以直线
为对称轴，将
相关知识点
推荐套卷
细心观察下图，认真分析各式，然后解答问题．
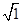()2+1=2 S1=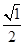、(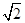)2+1=3 S2=、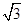（)2+1=4 S3=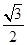
（1）推算出OA10的长；
（2）求出S12+S22+S32+…+S102的值．
粤公网安备 44130202000953号