为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的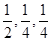 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求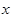 的分布列及期望。
的分布列及期望。
推荐套卷
为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的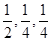 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求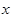 的分布列及期望。
的分布列及期望。