已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在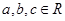 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且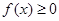 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。
相关知识点
推荐套卷
已知二次函数 .
.
(1)若 ,试判断函数
,试判断函数 零点个数;
零点个数;
(2)是否存在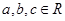 ,使
,使 同时满足以下条件
同时满足以下条件
①对任意 ,且
,且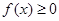 ;
;
②对任意 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(3)若对任意 且
且 ,
, ,试证明存在
,试证明存在 ,
,
使 成立。
成立。