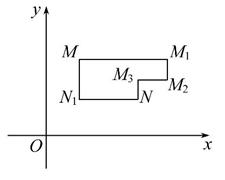
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建的居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.
(1)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明).
(2)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度之和最小.