通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| |
男 |
女 |
总计 |
| 看营养说明 |
50 |
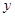 |
80 |
| 不看营养说明 |
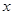 |
20 |
30 |
| 总计 |
60 |
50 |
 |
(1)根据以上表格,写出 的值.
的值.
(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
相关知识点
推荐套卷
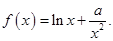
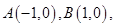 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且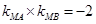 .
.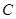 的方程;
的方程;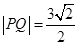 ,求直线PQ的方程.
,求直线PQ的方程.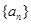 满足
满足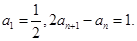
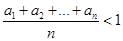 .
.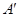 .
.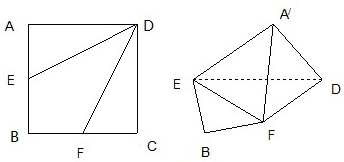
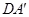 ⊥EF;
⊥EF;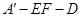 的平面角的余弦值.
的平面角的余弦值.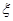 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号