如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,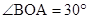
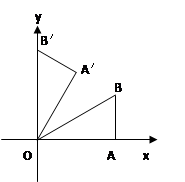
(1)求点B和点A′的坐标;
(2)求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。
相关知识点
推荐套卷
如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,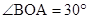
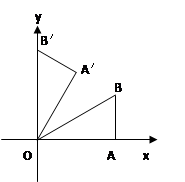
(1)求点B和点A′的坐标;
(2)求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。